QUANTUM SIMULATOR WITH RYDBERG ATOMS
Quantum computation and simulation distinguishable by the need for error correction can be further classified into two types, the analog (problem-based designed operations) and the digital (universal gate-based operations). In some situation where a set of universal gates is incomplete, and hence the error correction and fault tolerance are not guaranteed, then a problem-solving procedure must be specifically redesigned for each quantum many-body system of interest. It is where a digital quantum computer is regarded as a digital quantum simulator, which is an experimental system that mimic simple models. Useful quantum computer and simulator must be 1) relevant to applications and/or understanding 2) able to control over state preparation, initialization, manipulation, evolution, and detection 3) statistical within a prescribed error / reliability 4) more efficient than a classical counterpart does.
Quantum simulation uses a single well-controlled quantum system to simulate another complex many-body quantum system in regimes that are impossible to realize using conventional materials, e.g., condensed-matter physics, high-energy physics, atomic physics, quantum chemistry and cosmology where classical methods to model the system fail.
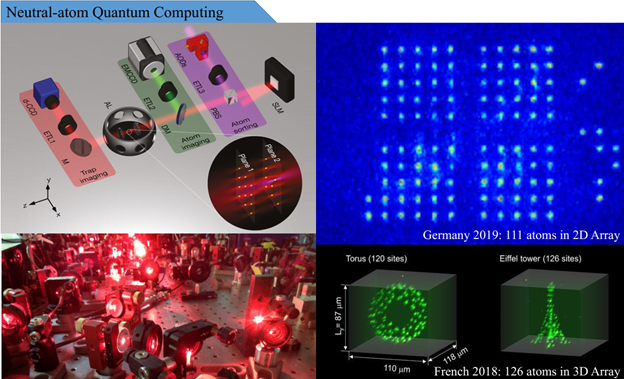
Quantum Tech: Because of the long coherence times, interaction tunability of Rydberg states, large polarizability (µn7), long lifetime (µn3), 3D-array producibility, manifold internal degrees of freedom, and flexibility in the trapping arrangement and geometry, dexterity to interrogate and manipulate, and parallel operations and qbit addressability which are natural in the lattice geometry; neutral atoms are considered a potential contender for both digital and analog quantum simulations. Our approach starts with defining qubits utilizing motional and internal states of the trap geometry and internal structure of cold single atoms. A 2D optical trap arrays are created from far-off-resonance red-detuned light. Standard laser spectroscopy is employed to prepare atoms in a desired fiducial state, implement coherent controls and couple atoms via dipole-dipole interaction. The trap itself and additional fields make available a variety of “handles” for coherent control of the motional and internal states. Raman sideband cooling in individual trap is necessary but not during the gate operations. The Hamiltonian premeditatedly engineered to mimic a selected physical system is implement using laser pulses and external fields. At the end of applying series of gate operations, measurements are separately performed on each atom.
Direct Societal Impact: Problems which are theoretically and numerically intractable, e.g., realizing Hubbard or transverse-field Ising Hamiltonian, simulate Haldane model and the Harper-Hofstadter model, identifying novel quantum phases, tracking out-of-equilibrium dynamics etc.
Collateral Advantages: –
Alternative Quantum Technology: Polar molecules, trapped ions, photonic systems, electrons in semiconductor including quantum dots, and superconducting circuits.
Aided System: –